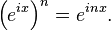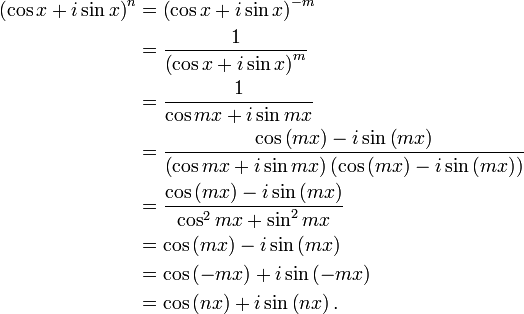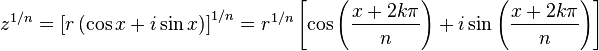Dalam matematika, de Moivre's formula, dinamai Abraham de Moivre, menyatakan bahwa untuk setiap bilangan kompleks (dan, khususnya, untuk setiap bilangan riil) x dan bilangan bulat n itu menyatakan bahwa
Rumusnya adalah penting karena menghubungkan bilangan kompleks (i melambangkan satuan imajiner) dan trigonometri. Ungkapan "cos x + i sin x" kadang-kadang disingkat menjadi "cis x".
Dengan memperluas sisi kiri dan kemudian membandingkan yang nyata dan imajiner bagian bawah asumsi bahwa x adalah nyata, itu adalah mungkin untuk mendapatkan ekspresi berguna bagi cos (nx) dan dosa (nx) dalam hal cos (x) dan dosa (x ). Lebih jauh lagi, orang dapat menggunakan generalisasi dari rumus ini untuk menemukan ekspresi eksplisit untuk n-th akar persatuan, yaitu bilangan kompleks z z sedemikian sehingga n = 1
Derivation
Meskipun sebelumnya terbukti secara historis, de Moivre's formula dapat dengan mudah diperoleh dari Rumus Euler
dan hukum eksponensial untuk integer kekuatan
Kemudian, dengan rumus Euler,
Kegagalan untuk non-integer kekuasaan
De Moivre's formula pada umumnya tidak berlaku untuk non-integer kekuasaan. Non-integer kekuatan nomor yang kompleks dapat memiliki banyak nilai yang berbeda, lihat kegagalan kekuasaan dan logaritma identitas. Namun ada generalisasi bahwa ekspresi sisi kanan adalah salah satu nilai mungkin kekuasaan.
Derivasi dari de Moivre's formula di atas melibatkan kompleks kekuasaan angka ke n. Ketika kekuasaan bukan integer, hasilnya adalah beberapa bernilai, misalnya, jika n = ½ maka:
Untuk x = 0 rumus memberikan 1 ½ = 1
Untuk x = 2 π rumus memberikan 1 ½ = -1
Karena sudut 0 dan 2π adalah sama dua ini akan memberikan nilai yang berbeda untuk ekspresi yang sama. Nilai-nilai 1 dan -1 Namun kedua adalah akar kuadrat dari 1 sebagai generalisasi menegaskan.
Tidak ada masalah seperti terjadi dengan Rumus Euler karena tidak ada identifikasi nilai-nilai yang berbeda dari eksponen. Rumus Euler melibatkan kekuatan kompleks bilangan real positif dan ini selalu memiliki nilai lebih disukai. Ekspresi yang sesuai:
e i 0 = 1
e iπ = -1
Derivasi dari de Moivre's formula di atas melibatkan kompleks kekuasaan angka ke n. Ketika kekuasaan bukan integer, hasilnya adalah beberapa bernilai, misalnya, jika n = ½ maka:
Untuk x = 0 rumus memberikan 1 ½ = 1
Untuk x = 2 π rumus memberikan 1 ½ = -1
Karena sudut 0 dan 2π adalah sama dua ini akan memberikan nilai yang berbeda untuk ekspresi yang sama. Nilai-nilai 1 dan -1 Namun kedua adalah akar kuadrat dari 1 sebagai generalisasi menegaskan.
Tidak ada masalah seperti terjadi dengan Rumus Euler karena tidak ada identifikasi nilai-nilai yang berbeda dari eksponen. Rumus Euler melibatkan kekuatan kompleks bilangan real positif dan ini selalu memiliki nilai lebih disukai. Ekspresi yang sesuai:
e i 0 = 1
e iπ = -1
Bukti dengan induksi (untuk integer n)
Untuk n> 0, kita melanjutkan dengan induksi matematika. Jika n = 1, hasilnya adalah jelas benar. Hipotesis kami, kami menganggap hasilnya adalah benar untuk beberapa bilangan bulat positif k. Artinya, kita asumsikan
Sekarang, mengingat kasus n = k + 1:
Kami menyimpulkan bahwa hasil itu benar untuk n = k + 1 saat itu benar untuk n = k. Dengan prinsip induksi matematika maka hasilnya adalah benar untuk semua bilangan bulat positif n ≥ 1.
Jika n = 0 rumus ini benar sejak cos (0 x) + i sin (0 x) = 1 + i 0 = 1.
Jika n <0, kami mempertimbangkan bilangan bulat positif m sedemikian sehingga n = - m. Sehingga
Jika n = 0 rumus ini benar sejak cos (0 x) + i sin (0 x) = 1 + i 0 = 1.
Jika n <0, kami mempertimbangkan bilangan bulat positif m sedemikian sehingga n = - m. Sehingga
leh karena itu, teorema adalah benar untuk semua bilangan bulat n nilai.
Rumus untuk kosinus dan sinus individual
Menjadi persamaan bilangan kompleks, orang perlu memiliki kesamaan baik dari bagian riil dan dari bagian imajiner dari kedua anggota persamaan. Jika x, dan oleh karena itu juga cos x dan sin x, adalah bilangan real, maka identitas bagian-bagian ini dapat ditulis (interchanging sisi) sebagai
Persamaan ini bahkan sebenarnya berlaku untuk nilai-nilai yang kompleks dari x, karena kedua belah pihak seluruh (yaitu, holomorphic pada seluruh bidang kompleks) fungsi dari x, dan dua fungsi seperti yang bertepatan pada sumbu nyata harus bertepatan di mana-mana. Berikut adalah contoh-contoh konkret persamaan ini untuk n = 2 dan n = 3:
Sisi sebelah kanan dari rumus untuk cos (nx) sebenarnya nilai T n (cos x) dari polinomial Chebyshev T n pada cos x.
Generalisasi
Rumus sebenarnya benar dalam pengaturan yang lebih umum daripada yang dinyatakan di atas: jika z dan w adalah bilangan kompleks, maka
adalah fungsi bernilai multi sementara
tidak. Oleh karena itu kita dapat menyatakan bahwa
Aplikasi
Formula ini dapat digunakan untuk menemukan akar ke-n dari bilangan kompleks. Aplikasi ini tidak secara tegas menggunakan de Moivre's formula sebagai kekuatan bukan integer. Namun mengingat sisi kanan n kekuatan dalam setiap kasus akan memberikan nilai yang sama sisi kiri.
Jika z adalah bilangan kompleks, ditulis dalam bentuk polar
Jika z adalah bilangan kompleks, ditulis dalam bentuk polar
kemudian
di mana k adalah integer, untuk mendapatkan akar n dari z berbeda satu hanya perlu mempertimbangkan nilai-nilai k dari 0 sampai n - 1.